Rozwiązanie układu równań w Microsoft Excel

Umiejętność rozwiązywania układów równań może często przynosić korzyści nie tylko w nauce, ale także w praktyce. Jednocześnie nie każdy użytkownik komputera wie, że istnieją własne warianty rozwiązywania równań liniowych w Excelu. Dowiedzmy się, jak wykonać to zadanie, używając różnych narzędzi tego procesora stołowego na różne sposoby.

Rozwiązania

Każde równanie można uznać za rozwiązane tylko wtedy, gdy zostaną znalezione jego korzenie. W Excelu istnieje kilka opcji wyszukiwania źródeł. Spójrzmy na każdego z nich.

Metoda 1: Metoda macierzy

Najczęstszym sposobem rozwiązania układu równań liniowych za pomocą narzędzi Excel jest użycie metody macierzowej. Polega ona na konstruowaniu macierzy współczynników wyrażeń, a następnie na tworzeniu macierzy odwrotnej. Spróbujmy użyć tej metody, aby rozwiązać następujący układ równań:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


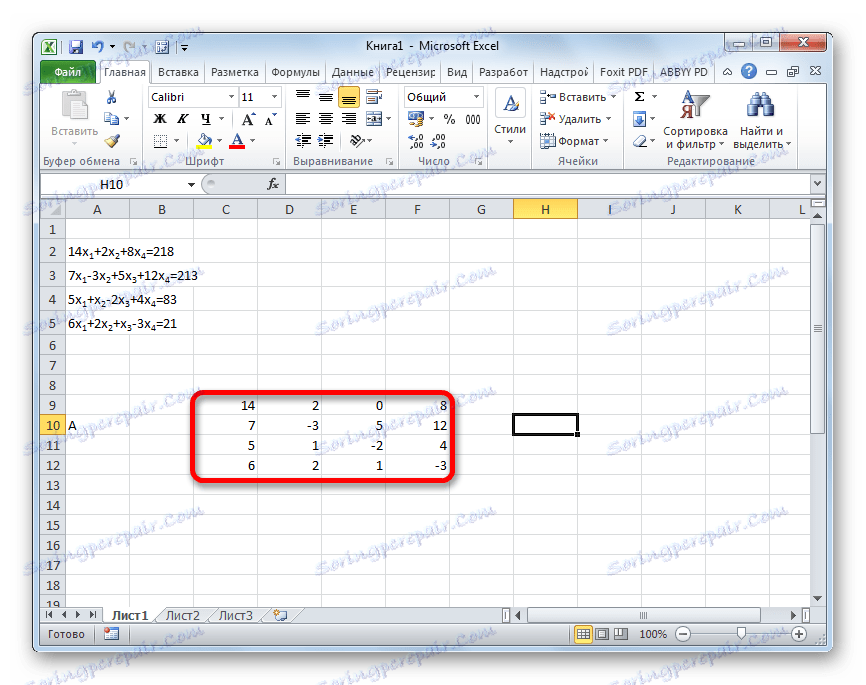
1. Wypełniamy macierz liczbami, które są współczynnikami równania. Numery te muszą być ułożone sekwencyjnie w kolejności, biorąc pod uwagę lokalizację każdego korzenia, do którego się odnoszą. Jeśli w jednym wyrażeniu brakuje jednego z korzeni, to w tym przypadku współczynnik uznaje się za równy zeru. Jeśli współczynnik nie jest wskazany w równaniu, ale odpowiadający mu pierwiastek jest obecny, przyjmuje się, że współczynnik wynosi 1 . Oznaczamy wynikową tabelę jako wektor A.
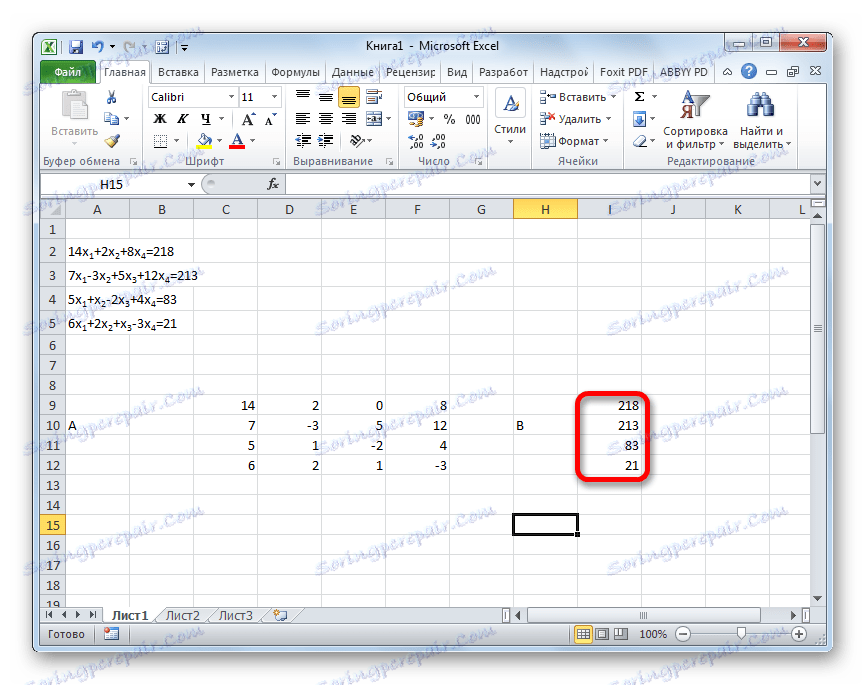
2. Osobno napisz wartości po znaku "równości". Oznacz je według ich wspólnej nazwy, jako wektor B.
3. Przede wszystkim, aby znaleźć korzenie równania, musimy znaleźć odwrotną macierz istniejącego. Na szczęście Excel ma specjalnego operatora, który ma na celu rozwiązanie tego problemu. Nazywa się ICBM . Ma dość prostą składnię:

   =МОБР(массив)

   Argument "Array" jest w rzeczywistości adresem tabeli źródłowej.

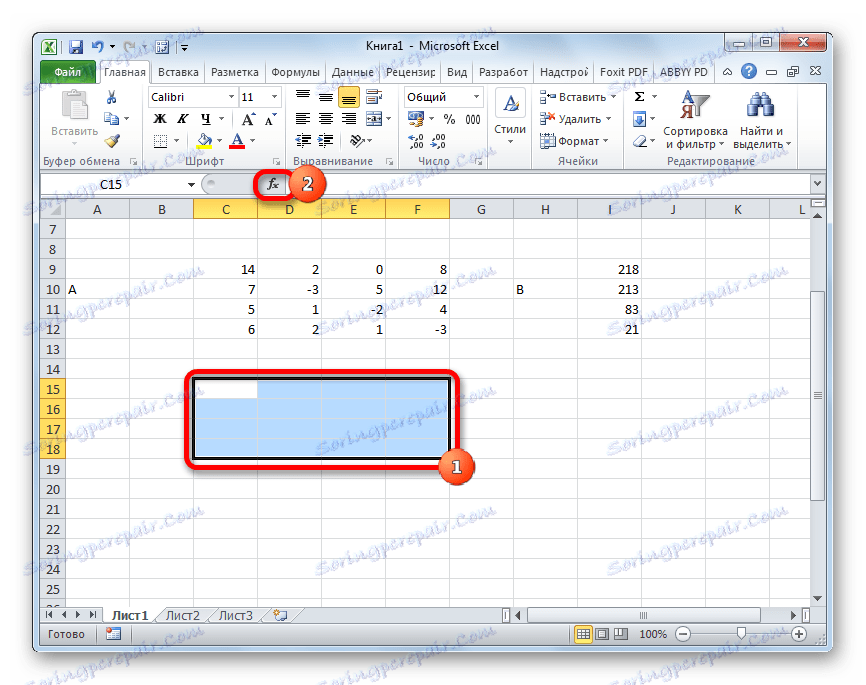
   Wybierzmy więc obszar pustych komórek na arkuszu, który jest równy rozmiarowi oryginalnej matrycy. Klikamy przycisk "Wstaw funkcję" , znajdujący się w pobliżu linii formuły.

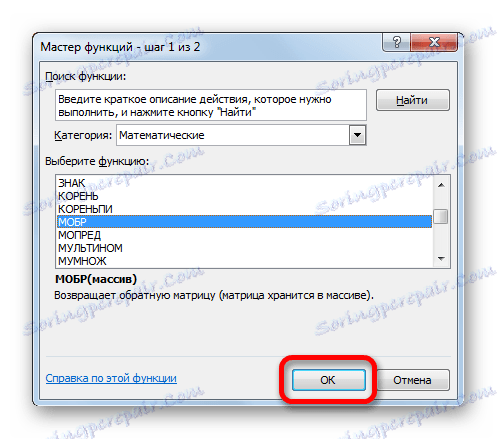
4. Uruchomi się Kreator funkcji . Przejdźmy do kategorii "Matematyczne" . Na przedstawionej liście szukamy nazwy "MOBR" . Po znalezieniu wybierz go i kliknij przycisk "OK" .
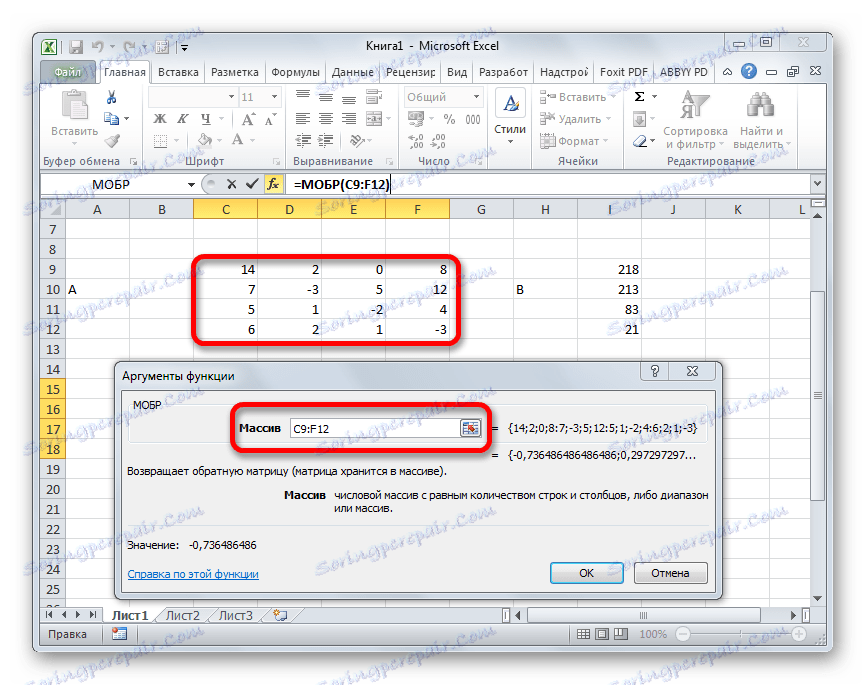
5. Otworzy się okno argumentu funkcji MOBR. Ma tylko jedno pole w liczbie argumentów - "Array" . Tutaj musisz podać adres naszej tabeli. W tym celu ustawiamy kursor w tym polu. Następnie przytrzymaj lewy przycisk myszy i wybierz obszar na arkuszu, w którym znajduje się matryca. Jak widać, dane o współrzędnych lokalizacji są automatycznie wprowadzane w polu okna. Po zakończeniu tego zadania najbardziej oczywiste będzie kliknięcie przycisku "OK" , ale nie spiesz się. Faktem jest, że kliknięcie tego przycisku jest równoważne użyciu polecenia Enter . Ale podczas pracy z tablicami po zakończeniu wprowadzania formuły nie powinieneś klikać przycisku Enter , ale tworzyć zestaw skrótów klawiaturowych Ctrl + Shift + Enter . Wykonujemy tę operację.
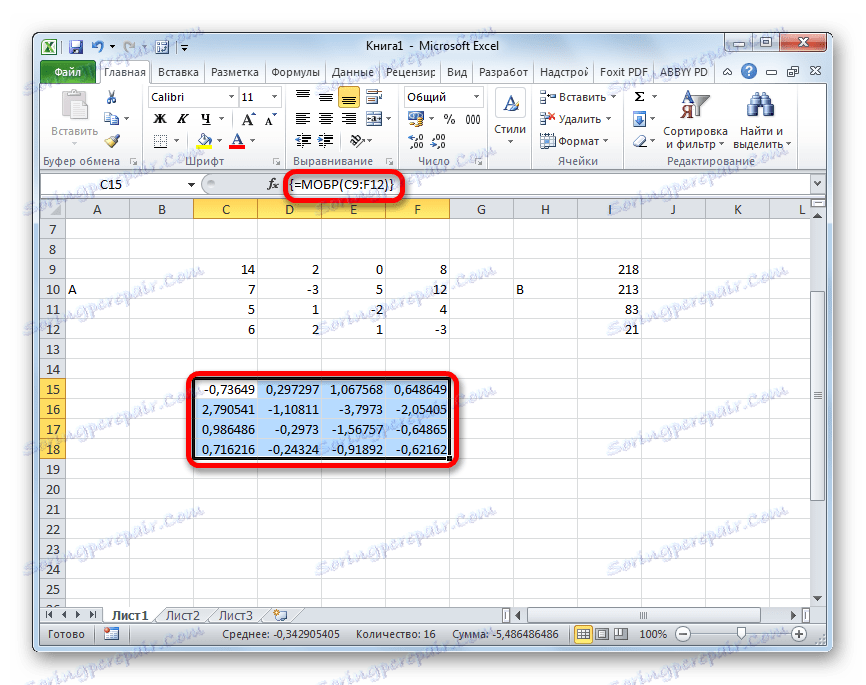
6. Następnie program wykonuje obliczenia, a na wyjściu w uprzednio przydzielonym obszarze mamy macierz odwrotną do tej.
7. Teraz musimy pomnożyć odwrotną macierz przez macierz B , która składa się z jednej kolumny wartości położonej za znakiem równości w wyrażeniach. Do mnożenia tabel w Excelu jest też osobna funkcja, która nazywa się LUDZKĄ . To oświadczenie ma następującą składnię:

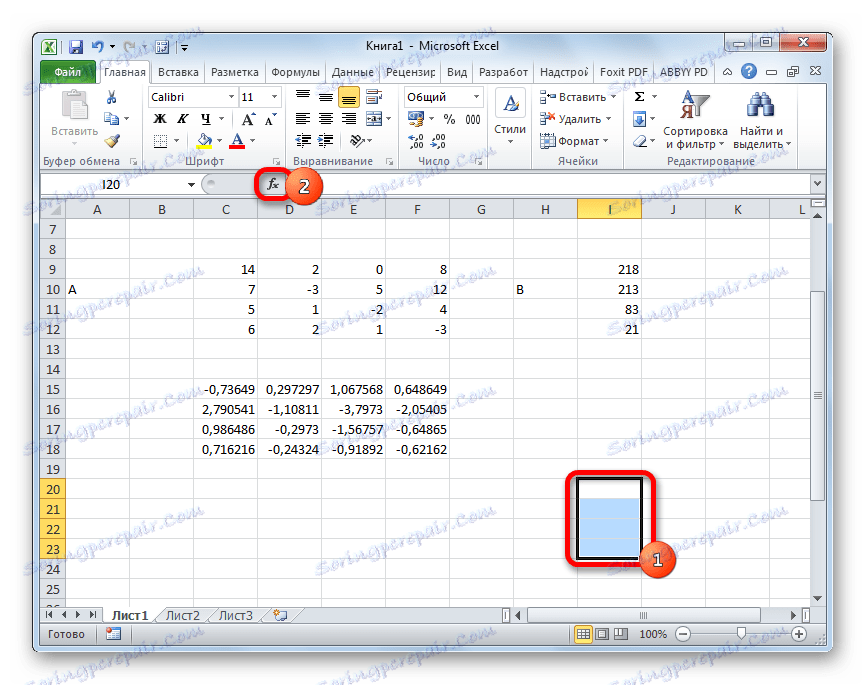
   =МУМНОЖ(Массив1;Массив2)

   Wybieramy zakres, w naszym przypadku składający się z czterech komórek. Następnie ponownie uruchom Kreatora funkcji , klikając ikonę "Wstaw funkcję" .

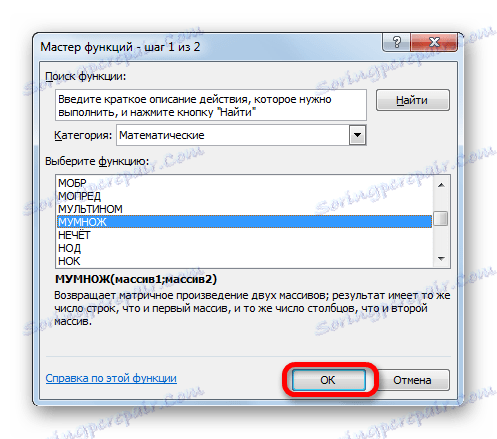
8. W kategorii "Matematyczny" , Uruchomiony Kreator funkcji , wybierz nazwę "HUMBLE" i kliknij przycisk "OK" .
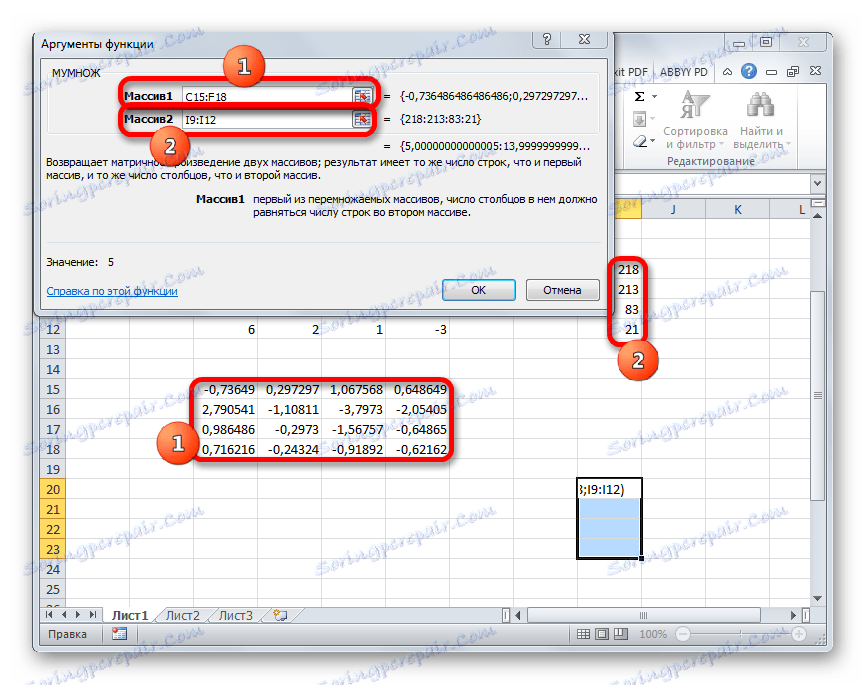
9. Okno argumentów funkcji MULTI . W polu "Array1" wpisujemy współrzędne naszej macierzy odwrotnej. W tym celu, podobnie jak w ostatnim czasie, ustawiamy kursor w polu i naciskając lewy przycisk myszy, wybierz odpowiednią tabelę za pomocą kursora. Wykonujemy podobną akcję, aby wprowadzić współrzędne w polu "Array2" , tylko tym razem wybieramy wartości z kolumny B. Po wykonaniu powyższych czynności, ponownie nie spiesz się, aby nacisnąć przycisk "OK" lub klawisz Enter , a następnie wpisz Ctrl + Shift + Enter .
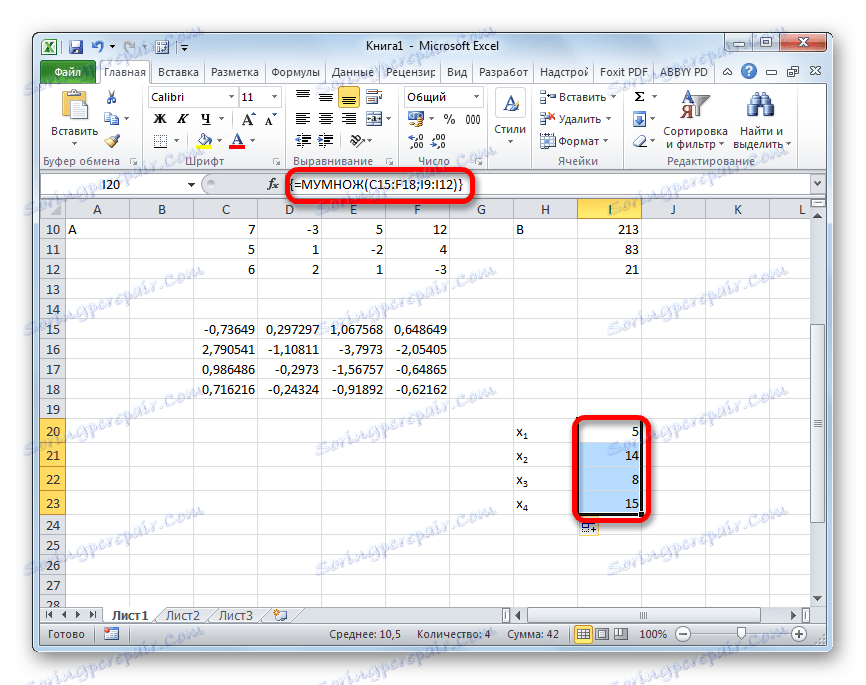
10. Po tym działaniu korzenie równania są wyświetlane w poprzednio wybranej komórce: X1 , X2 , X3 i X4 . Zostaną one ułożone sekwencyjnie. Tak więc możemy powiedzieć, że rozwiązaliśmy ten system. Aby zweryfikować poprawność rozwiązania, wystarczy podstawić te korzenie do oryginalnego systemu wyrażeń. Jeśli zaobserwujemy równość, oznacza to, że przedstawiony układ równań rozwiązany jest poprawnie.

Lekcja: Macierz odwrotna w Excelu

Metoda 2: wybór parametrów

Drugim znanym sposobem rozwiązania układu równań w Excelu jest zastosowanie metody wyboru parametrów. Istotą tej metody jest poszukiwanie przeciwieństwa. Oznacza to, że na podstawie znanego wyniku szukamy nieznanego argumentu. Wykorzystajmy równanie kwadratowe

3x^2+4x-132=0

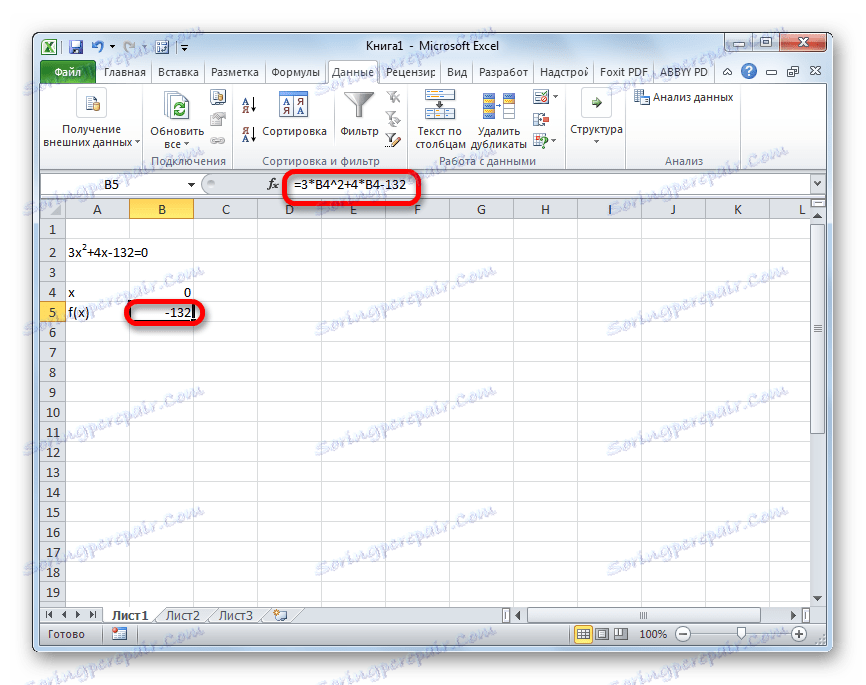
1. Załóżmy wartość x dla równego 0 . Obliczamy odpowiednią wartość f (x) , stosując następującą formułę:

   =3*x^2+4*x-132

   Zamiast wartości "X", wpisz adres komórki, gdzie znajduje się numer 0 , który przyjęliśmy dla x .

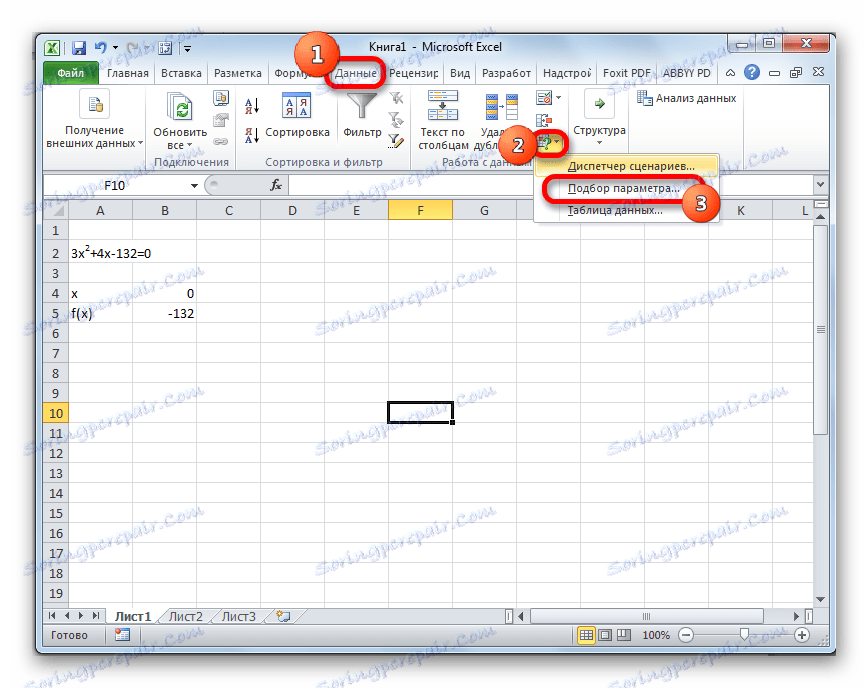
2. Przejdź do zakładki "Dane" . Kliknij przycisk "Analiza co jeśli" . Ten przycisk znajduje się na wstążce w oknie narzędzi "Praca z danymi" . Wyświetli się lista rozwijana. Wybierz pozycję "Wybór parametru ..." .
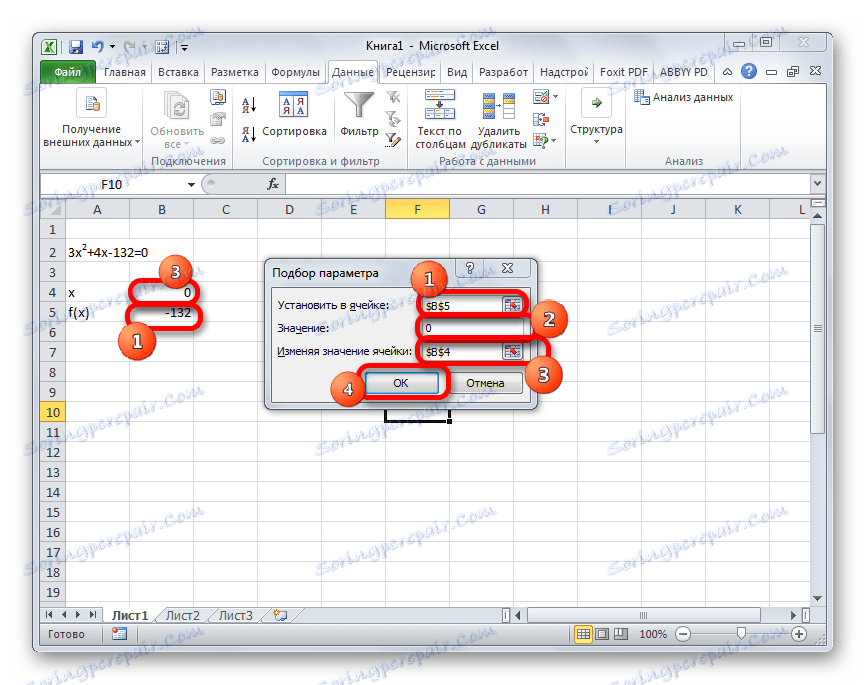
3. Otworzy się okno wyboru parametrów. Jak widać, składa się z trzech pól. W polu "Ustaw w komórce" określamy adres komórki, w której znajduje się obliczona przez nas formuła f (x) nieco wcześniej. W polu "Wartość" wpisz liczbę "0" . W polu "Zmiana wartości" wskazujemy adres komórki, w której znajduje się wartość x , którą wcześniej zajęliśmy dla 0 . Po wykonaniu tych kroków kliknij przycisk "OK" .
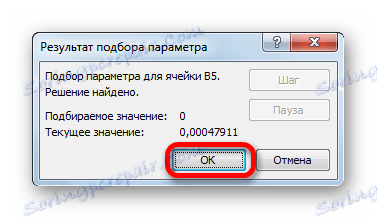
4. Następnie Excel wykona obliczenia, wybierając parametr. Zostanie to zgłoszone przez okno informacyjne, które się pojawiło. W tym celu kliknij przycisk "OK" .
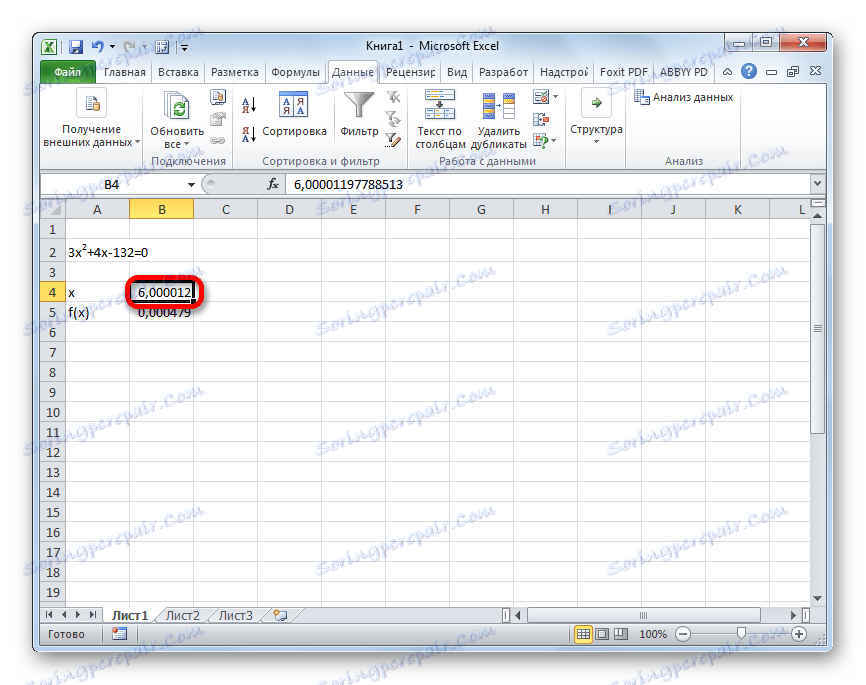
5. Wynik obliczenia pierwiastka równania będzie w komórce, którą wyznaczyliśmy w polu "Zmiana wartości" . W naszym przypadku, jak widzimy, x będzie równe 6 .

Ten wynik można również sprawdzić, zastępując tę ​​wartość w rozwiązanym wyrażeniu zamiast wartości x .

Lekcja: Wybór parametrów w Excelu

Metoda 3: Metoda Cramera

Teraz spróbujmy rozwiązać układ równań metodą Cramera. Na przykład weź ten sam system, który był używany w Trybie 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


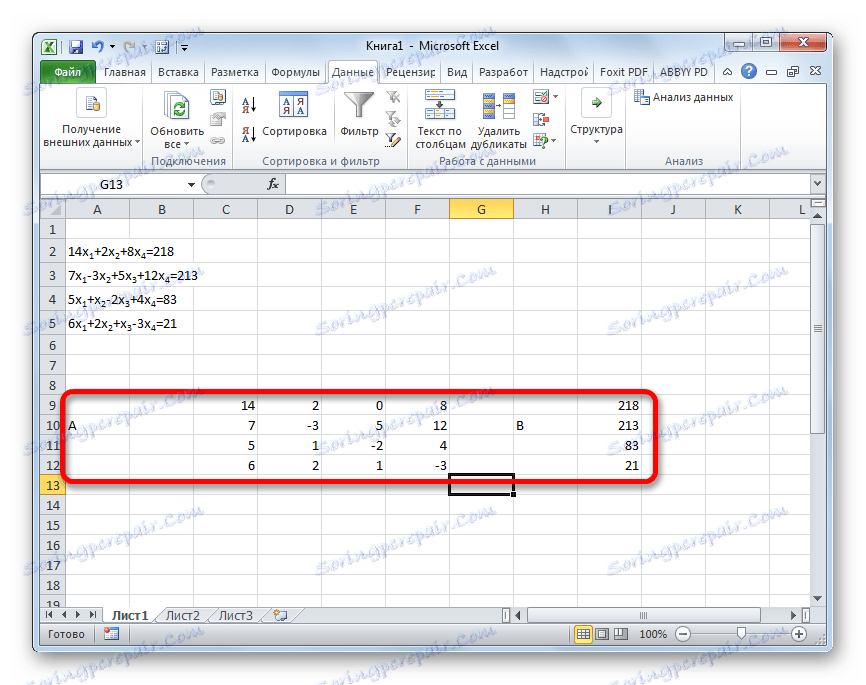
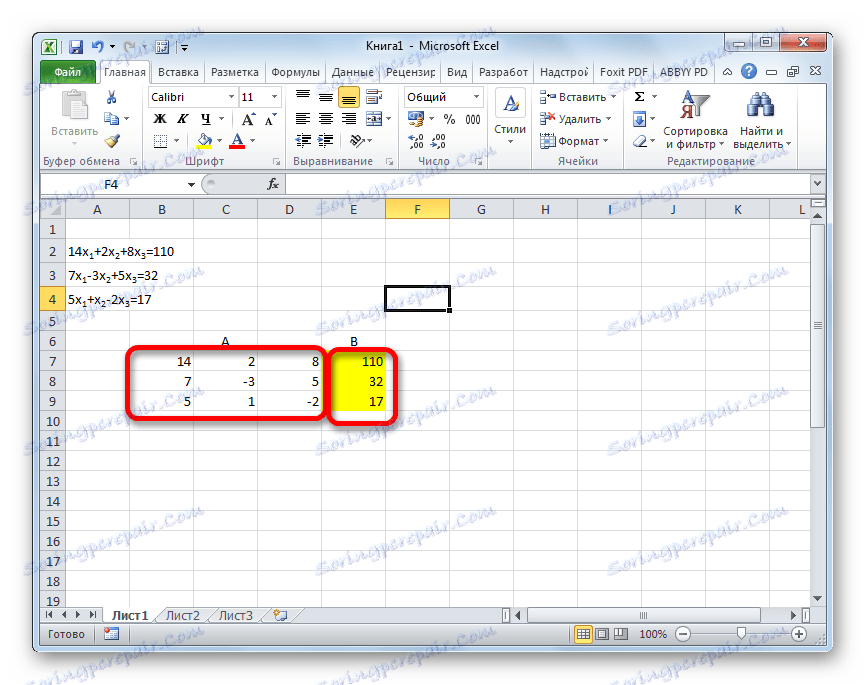
1. Podobnie jak w pierwszym sposobie, komponujemy macierz A ze współczynników równań i tabeli B z wartości, które stoją za znakiem "równości" .
2. Następnie tworzymy cztery kolejne tabele. Każda z nich jest kopią macierzy A , tylko dla tych kopii jedna kolumna jest zastępowana na przemian tablicą B. Pierwsza tabela ma pierwszą kolumnę, druga tabela ma drugą kolumnę i tak dalej.
3. Teraz musimy obliczyć wyznaczniki dla wszystkich tych tabel. Układ równań będzie miał rozwiązania tylko wtedy, gdy wszystkie wyznaczniki mają wartość różną od zera. Aby ponownie obliczyć tę wartość w programie Excel, istnieje osobna funkcja - MOPRED . Składnia tego operatora to:

   =МОПРЕД(массив)

   Tak więc, tak jak w przypadku funkcji MBD , jedynym argumentem jest odniesienie do przetwarzanej tabeli.

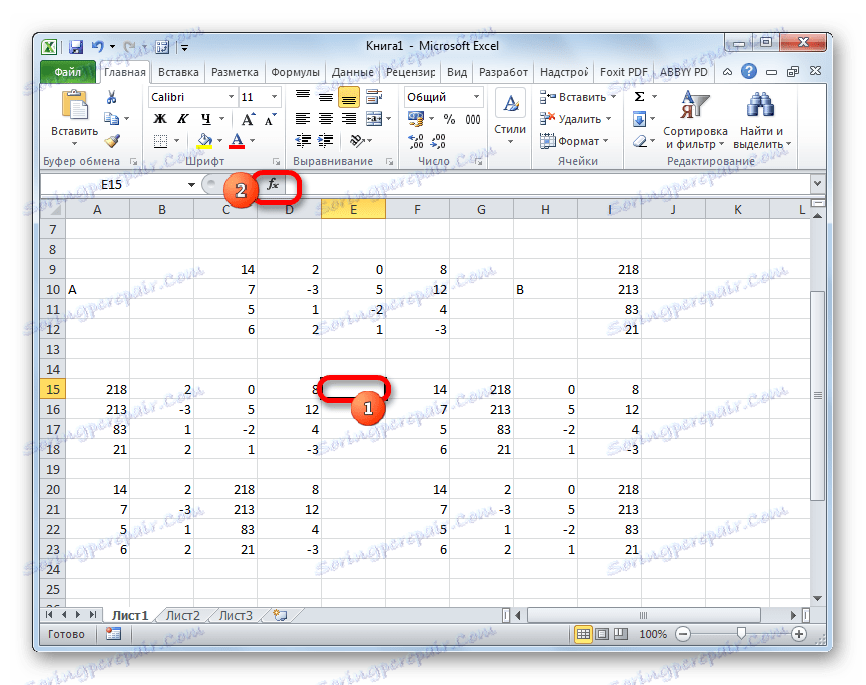
   Wybierz komórkę, w której zostanie wyświetlona wyznacznik pierwszej macierzy. Następnie kliknij przycisk "Wstaw funkcję" , który jest znany z poprzednich metod.

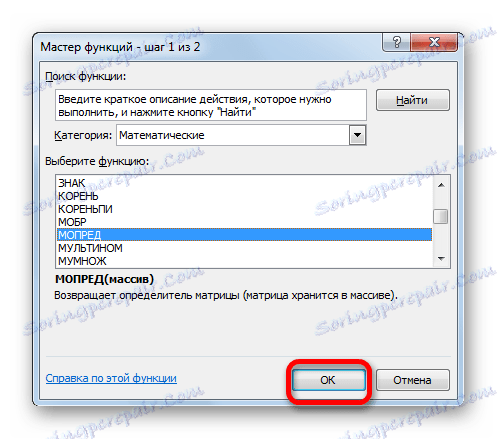
4. Okno Wizards zostanie aktywowane. Przechodzimy do kategorii "Matematyczne" i na liście operatorów wybieramy tam nazwę "MOPRED" . Następnie kliknij przycisk "OK" .
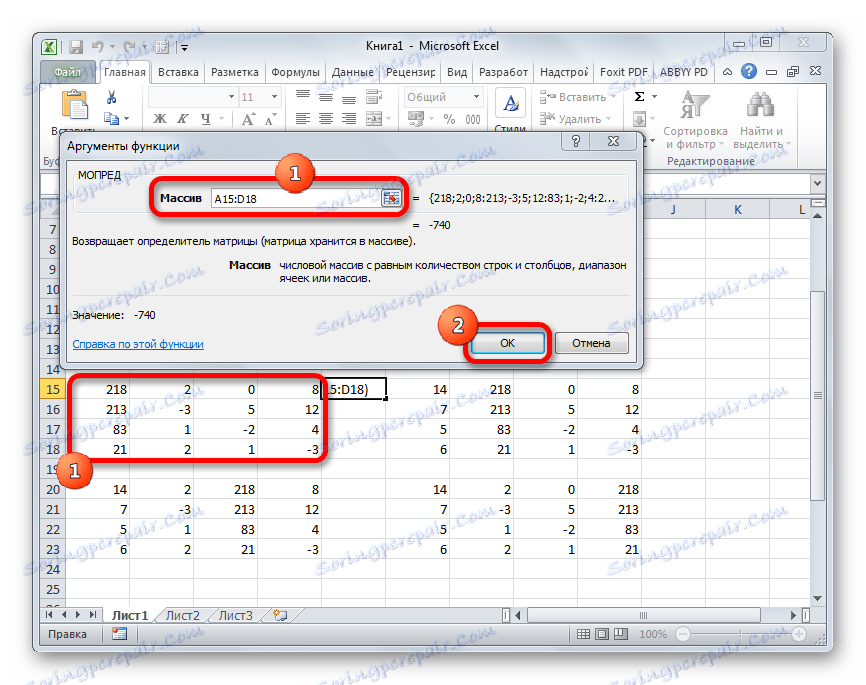
5. Otworzy się okno argumentów funkcji MOPED . Jak widać, ma tylko jedno pole - "Array" . W tym polu wpisujemy adres pierwszej przekształconej macierzy. Aby to zrobić, ustaw kursor w polu, a następnie wybierz zakres macierzy. Następnie kliknij przycisk "OK" . Ta funkcja wyświetla wynik w jednej komórce, a nie w tablicy, więc nie trzeba naciskać Ctrl + Shift + Enter, aby uzyskać obliczenia.
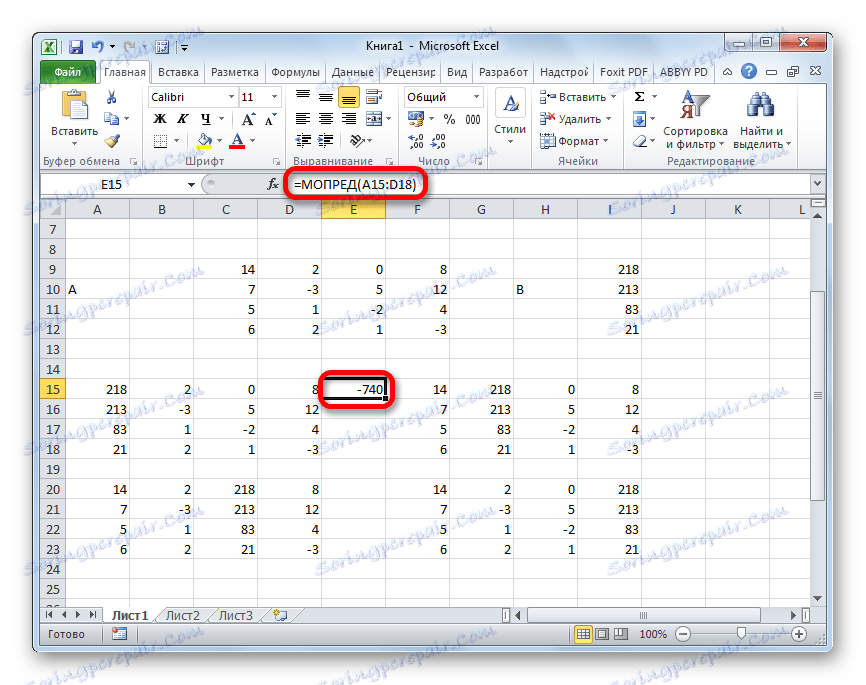
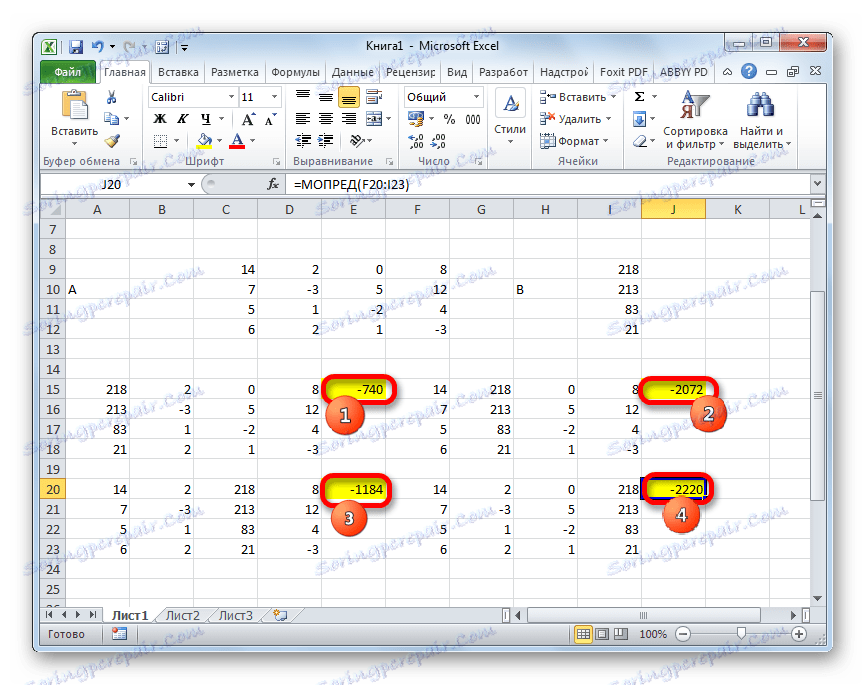
6. Funkcja oblicza wynik i wyprowadza go do wcześniej wybranej komórki. Jak widać, w naszym przypadku wyznacznikiem jest -740 , czyli nie jest równy zeru, który jest odpowiedni dla nas.
7. Podobnie obliczamy wyznaczniki dla pozostałych trzech tabel.
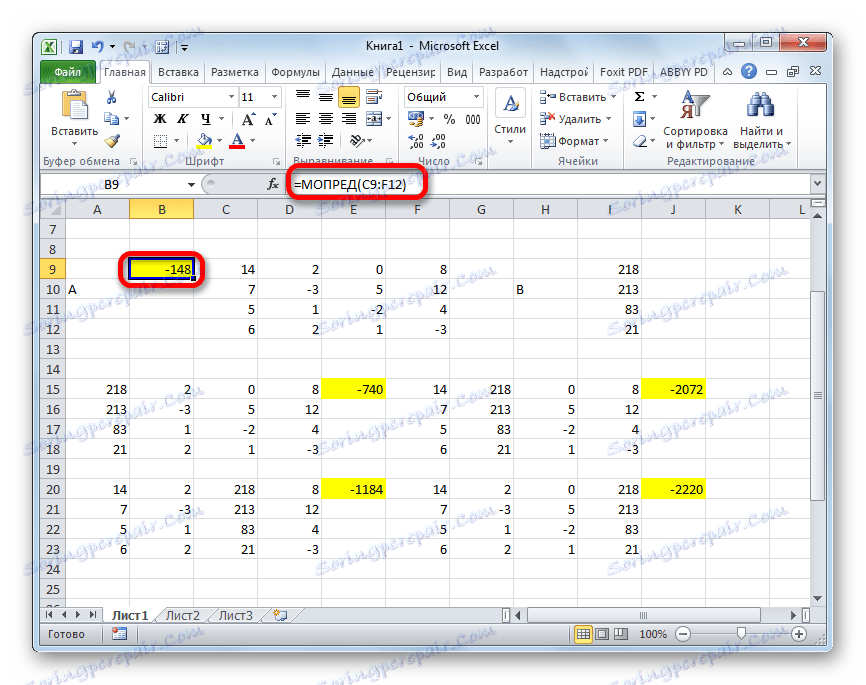
8. Na ostatnim etapie obliczamy wyznacznik macierzy pierwotnej. Procedura jest taka sama dla tego samego algorytmu. Jak widać, wyznacznik tabeli podstawowej również jest różny od zera, a zatem macierz jest uważana za nieegeneratywną, czyli system równań ma rozwiązania.
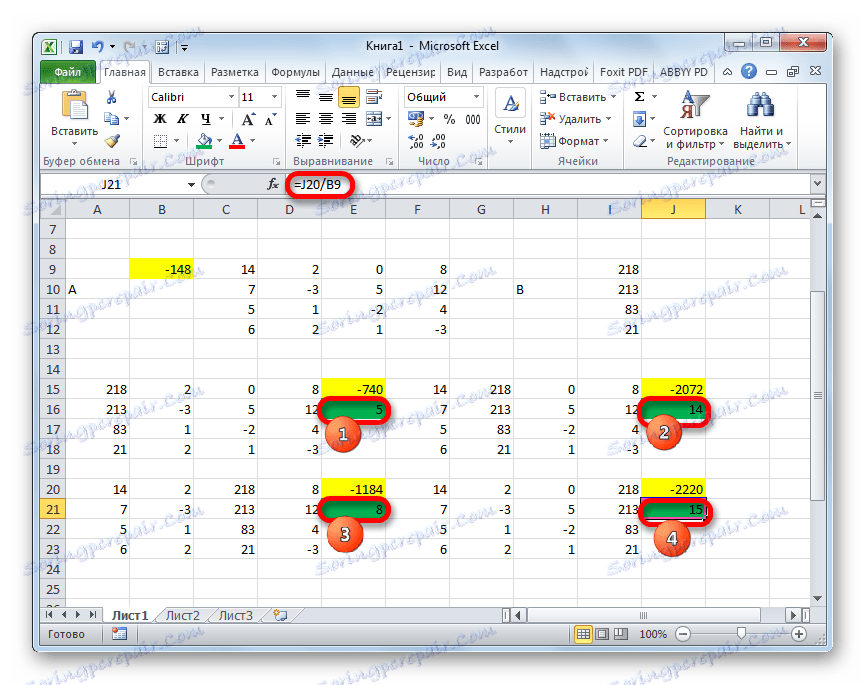
9. Teraz czas znaleźć korzenie równania. Korzeń równania będzie równy stosunkowi wyznacznika odpowiedniej transformowanej macierzy do wyznacznika tabeli głównej. Zatem po podzieleniu wszystkich czterech wyznaczników transformowanych macierzy jeden po drugim -148 , który jest wyznacznikiem oryginalnej tabeli, otrzymujemy cztery korzenie. Jak widać, są one równe wartościom 5 , 14 , 8 i 15 . W związku z tym dokładnie pokrywają się one z korzeniami, które znaleźliśmy za pomocą macierzy odwrotnej w metodzie 1 , która potwierdza poprawność rozwiązania układu równań.

Metoda 4: Metoda Gaussa

Rozwiąż system równań można również wykonać za pomocą metody Gaussa. Na przykład, weźmy prostszy układ równań trzech niewiadomych:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. Ponownie rejestrujemy kolejno współczynniki w Tabeli A i wolne terminy znajdujące się po znaku "równości" w Tabeli B. Ale tym razem przybliżymy obie tabele, ponieważ będzie to konieczne, abyśmy mogli pracować w przyszłości. Ważnym warunkiem jest to, że w pierwszej komórce macierzy A wartość jest różna od zera. W przeciwnym przypadku należy rozmieścić rzędy w miejscach.
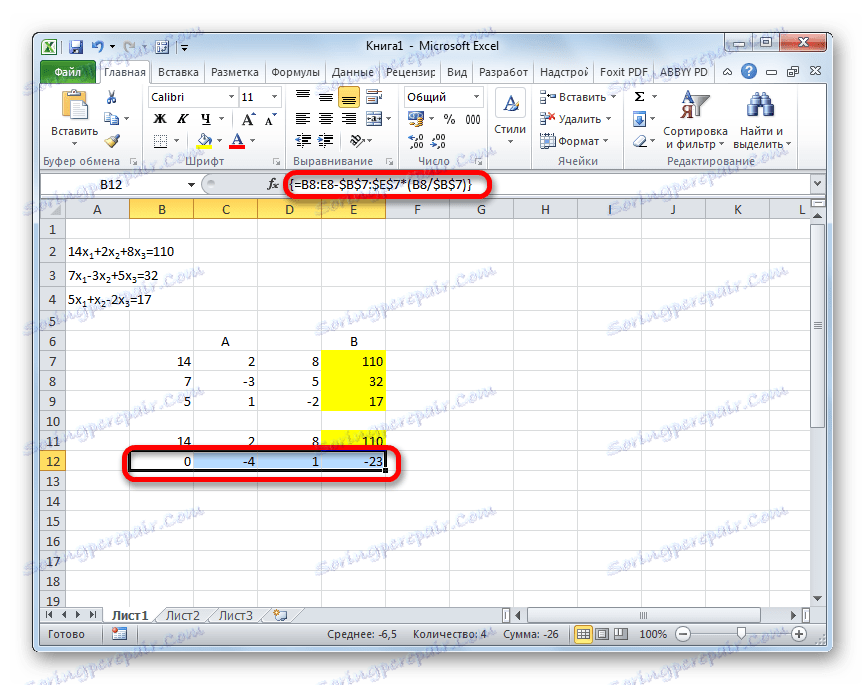
2. Skopiuj pierwszy wiersz dwóch połączonych macierzy w rzędzie poniżej (dla jasności możesz pominąć jedną linię). W pierwszej komórce, która znajduje się w rzędzie jeszcze niższej niż poprzednia, wpisujemy następującą formułę:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Jeśli rozmieszczasz macierze w inny sposób, adresy komórek formuły będą miały dla ciebie inną wartość, ale możesz je obliczyć, porównując je ze wzorami i obrazami, które są tutaj podane.

   Po wprowadzeniu formuły zaznacz cały wiersz komórek i naciśnij Ctrl + Shift + Enter . Formuła tablicy zostanie zastosowana do wiersza i zostanie wypełniona wartościami. Odejmujemy więc od drugiej linii pierwszą, pomnożoną przez stosunek pierwszych współczynników dwóch pierwszych wyrażeń układu.

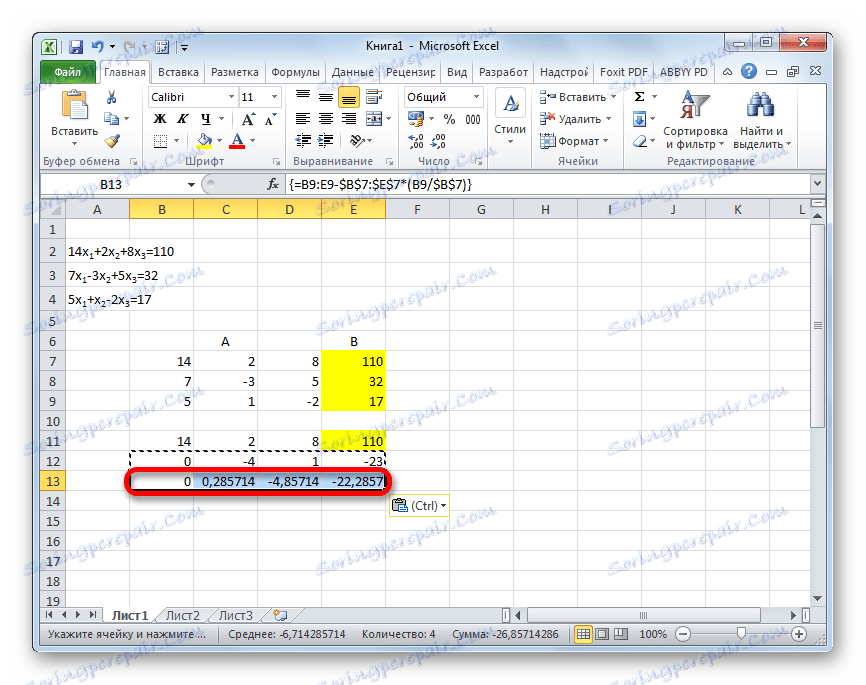
3. Następnie skopiuj wynikową linię i wklej ją w wierszu poniżej.
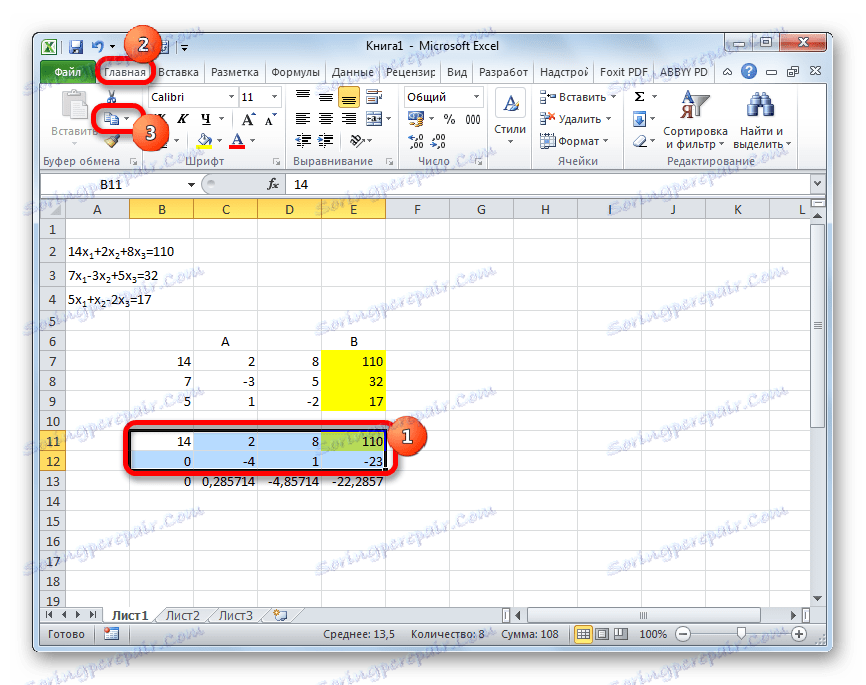
4. Wybierz pierwsze dwie linie za brakującą linią. Kliknij przycisk "Kopiuj" , który znajduje się na wstążce w zakładce "Strona główna" .
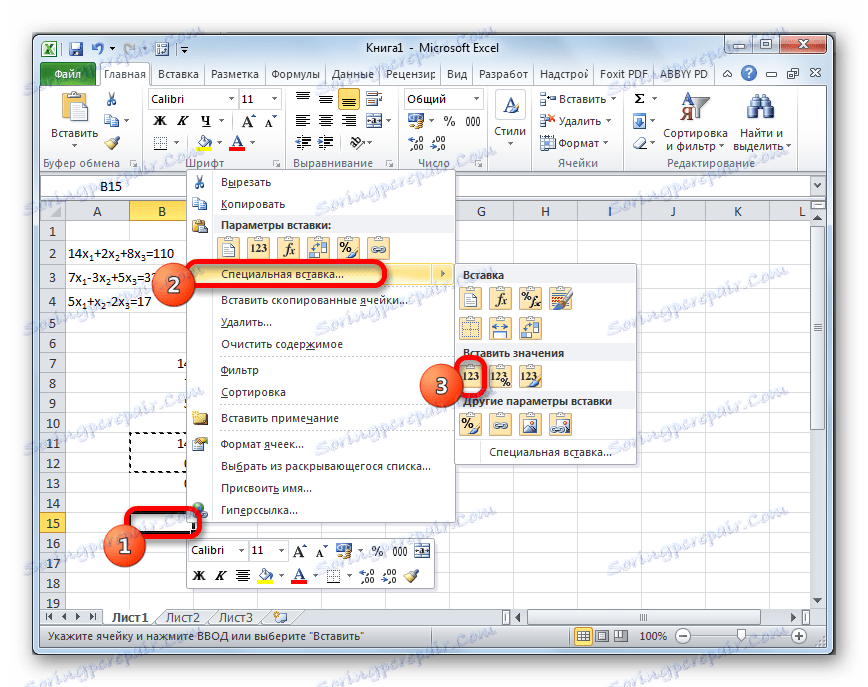
5. Pomijamy linię po ostatnim zapisie na arkuszu. Wybierz pierwszą komórkę w następnym wierszu. Kliknij prawym przyciskiem myszy. W otwartym menu kontekstowym ustawiamy kursor nad pozycją "Pasta specjalna" . Na dodatkowej liście, która się zaczyna, wybierz pozycję "Wartości" .
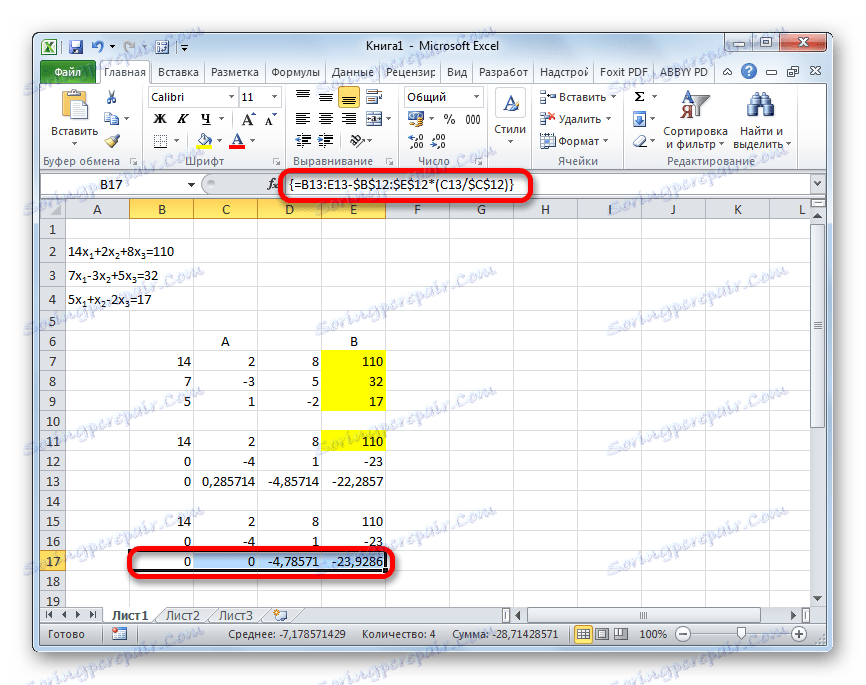
6. W następnym wierszu wprowadź formułę tablicy. Odejmuje drugi wiersz od trzeciego wiersza poprzedniej grupy danych, pomnożony przez stosunek drugiego współczynnika z trzeciego i drugiego wiersza. W naszym przypadku formuła będzie miała następującą formę:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Po wprowadzeniu formuły zaznacz całą serię i zastosuj skrót klawiaturowy Ctrl + Shift + Enter .

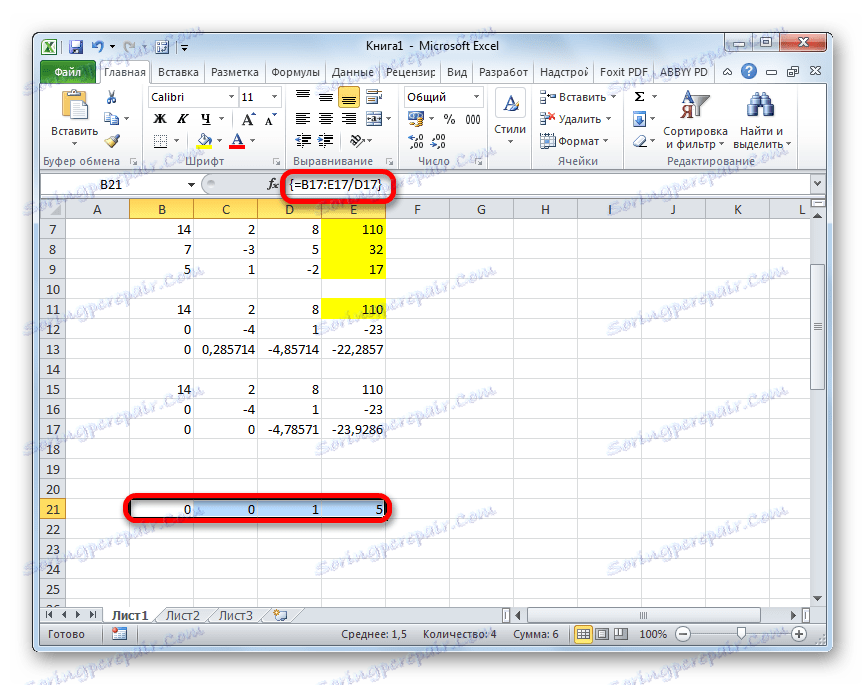
7. Teraz konieczne jest wykonanie odwróconego przebiegu za pomocą metody Gaussa. Pomijamy trzy linie z ostatniej płyty. W czwartym wierszu wpisujemy formułę tablicy:

   =B17:E17/D17

   W ten sposób dzielimy ostatnią linię, którą obliczyliśmy przez jej trzeci współczynnik. Po wpisaniu formuły wybierz całą linię i naciśnij Ctrl + Shift + Enter .

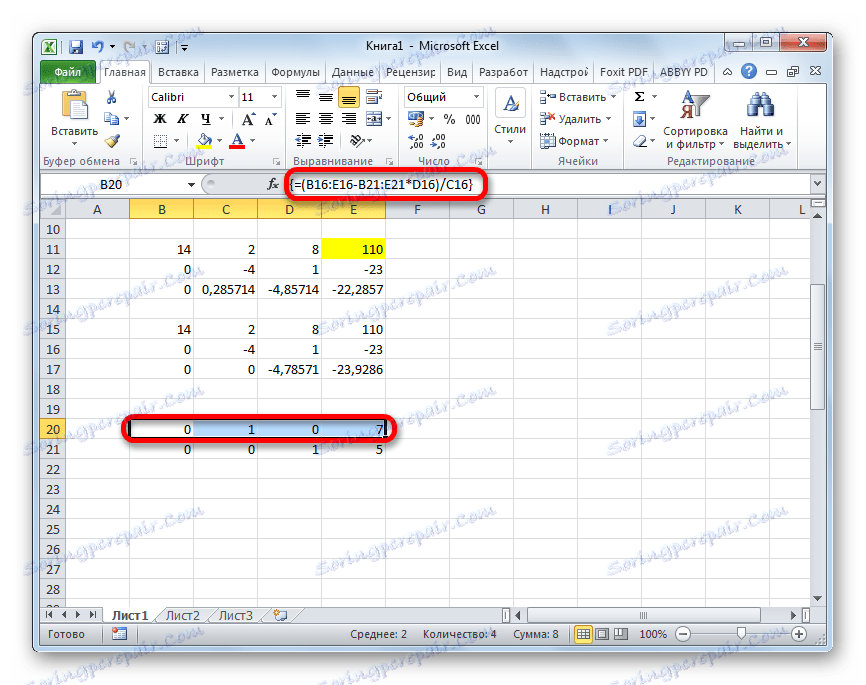
8. Podnosimy linię do góry i wprowadzamy do niej następującą formułę tablicy:

   =(B16:E16-B21:E21*D16)/C16

   Naciskamy zwykłą kombinację klawiszy, aby zastosować formułę tablicową.

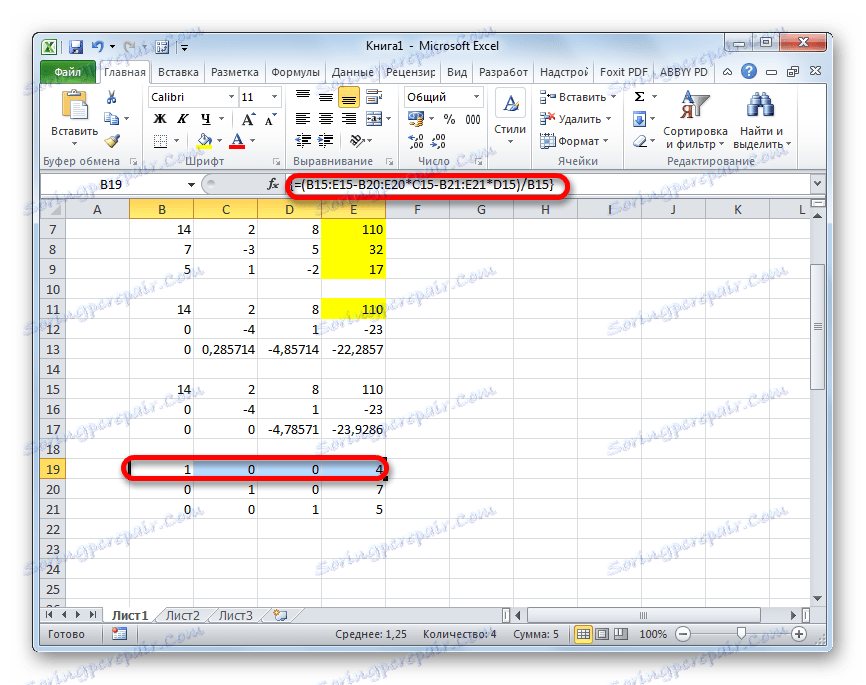
9. Podnosimy o jedną linię wyżej. W nim wpisujemy formułę tablicy następującej postaci:

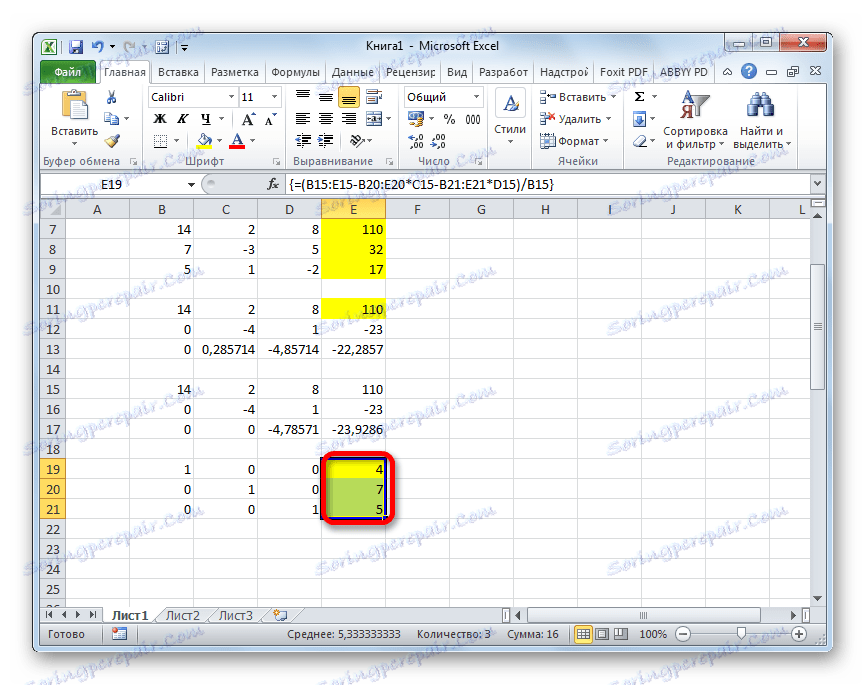
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Ponownie wybierz całą linię i zastosuj kombinację klawiszy Ctrl + Shift + Enter .

10. Teraz spójrz na liczby, które zostały uzyskane w ostatniej kolumnie ostatniego bloku linii, obliczonego przez nas wcześniej. To właśnie te liczby ( 4 , 7 i 5 ) będą korzeniami danego układu równań. Możesz to sprawdzić, zastępując je wyrażeniami X1 , X2 i X3 .

Jak widać, w Excelu system równań można rozwiązać za pomocą wielu metod, z których każda ma swoje zalety i wady. Ale wszystkie te metody można warunkowo podzielić na dwie duże grupy: macierz i za pomocą narzędzia do wyboru parametrów. W niektórych przypadkach nie zawsze metody matrycowe są odpowiednie do rozwiązania problemu. W szczególności, gdy wyznacznik macierzy wynosi zero. W innych przypadkach użytkownik może zdecydować, która opcja jest dla niego wygodniejsza.

• ← Budowanie paraboli w programie Microsoft Excel
• Tworzenie przycisku w programie Microsoft Excel →